奈奎斯特图:图、稳定性、示例问题及其应用
波德图和奈奎斯特图是非常受欢迎的图,尤其是电化学阻抗谱或电化学阻抗谱数据。因此,奈奎斯特阴谋是以一位瑞典裔美国人“哈里·奈奎斯特”的名字命名的。他是。。。
波德图和奈奎斯特图是非常受欢迎的图,尤其是电化学阻抗谱或电化学阻抗谱数据。因此,奈奎斯特阴谋是以一位瑞典裔美国人“哈里·奈奎斯特”的名字命名的。他是一名电气工程师,于1932年开发了这幅用于电子目的的地块。在环境影响报告期间,收集了大量信息,这些收集的信息需要呈现出来。因此,一张图片提供的信息比一百个单词还要多。因此,像奈奎斯特图这样的图形表示被用来显示电化学阻抗谱。本文提供了有关的信息奈奎斯特图–工作、优点和缺点。
奈奎斯特图定义
被广泛用于传递函数的图形表示被称为奈奎斯特图。这是一个频率响应图,用于评估具有反馈稳定性的控制系统。它是复平面内传递函数实部和虚部的参数图,因为频率参数在指定的区间内扫描。在笛卡尔坐标系中,奈奎斯特图传递函数的实部绘制在X轴上,而传递函数的虚部绘制在Y轴上。
奈奎斯特图用于自动控制以及用于稳定性分析的信号处理,因为任何人都可以立即验证具有负反馈的回路是否符合奈奎斯特的稳定性原理。如果开环控制系统的奈奎斯特图大致覆盖了随后实轴上的点,则等效闭环系统是不稳定的。
奈奎斯特曲线图
奈奎斯特图是极坐标图的扩展,主要用于通过简单地将“ω”从-∞变为∞来寻找闭环控制系统的稳定性。也就是说,这些图主要用于绘制开环传递函数的总频率响应。奈奎斯特图简单地通过反馈来评估控制系统的稳定性。因此,在笛卡尔坐标系中,传递函数的实数部分简单地绘制在X轴上,而虚数部分简单地画在Y轴上。
类似的奈奎斯特图可以用极坐标简单地解释,其中传递函数的增益是径向坐标,传递函数的相位是等效角坐标。
奈奎斯特图可以通过了解所使用的一些术语来理解。在奈奎斯特图中,复杂平面内的闭合路径称为轮廓。
奈奎斯特路径
奈奎斯特路径或奈奎斯特轮廓是s平面内的闭合轮廓,它完全包围了s平面的整个右侧。为了包围平面的总RHS,沿着“jω”轴和源中心的直径绘制了一个大的半圆车道。半圆半径被简单地视为奈奎斯特圆。
奈奎斯特包围
如果在曲线中找到一个点,就知道它被一条线包围了。
奈奎斯特映射
将s平面内的点变为F(s)平面内的一点的过程称为映射,F(s(s))称为映射的函数。
反馈控制系统的稳定性分析主要取决于识别s平面上特征方程的位置根。
因此,如果s平面上的根位于左侧面上,则控制系统是稳定的。因此,系统的相对稳定性可以通过不同的频率响应技术来确定,如奈奎斯特图、波德图和尼科尔斯图。
奈奎斯特稳定性准则
奈奎斯特稳定性准则主要用于识别特征方程在S平面特定区域中的根的存在性。像N=Z–P这样的奈奎斯特稳定性准则就是这么说的N’是关于原点的环绕总数,P’是极点的数量,Z’是零的总数。
在情况1中:当N=0(无包围)时,因此Z=P=0&Z=P。
如果N=0,则P应为“0”,因此系统是稳定的。
在情况2:当N大于0(顺时针环绕)时,因此P=0,Z≠0&Z>P
在这两种情况下,系统是不稳定的。
在情况3中:当N小于0(逆时针环绕)时,因此Z=0,P≠0&P>Z
因此,系统是稳定的。
如何绘制奈奎斯特图?
绘制奈奎斯特图涉及许多步骤,如下所述。
- 在步骤1中:需要检查极点的开环传递函数,如“s”平面内的G(s)H(s)。
- 在第2步中:通过简单地画一个半径为“R”的半圆,其中R趋于无穷大,选择正确的奈奎斯特轮廓,包括s平面的整个右侧。
- 在步骤3中:识别轮廓上的不同片段,并将其定位到奈奎斯特路径。
- 在步骤4中:映射段需要通过简单地替换映射函数中的各个段方程来执行整个段。一般来说,我们必须为特定的线段绘制极坐标图。
- 在步骤5中:通常,分段映射是正虚轴的特定路径的映射的反射图像。
- 在步骤6中:覆盖平面右半部分的半圆车道通常映射到G(s)H(s)平面内的一个点。
- 在步骤7中:将所有不同的映射段互连以产生必要的奈奎斯特图。
- 在步骤8中:记下顺时针围绕(-1,0)的圈数,并通过N=Z–P确定稳定性。
一旦绘制出奈奎斯特图,我们就可以用奈奎斯特稳定性准则来发现闭环控制系统的稳定性。因此,如果临界点(-1+j0)位于包围圈的外侧,那么闭环控制系统是完全稳定的。
开环传递函数是G(S)H(S)=N(S)/D(S)。
闭环传递函数是G(S)/1+G(S,H(S)。
N(s)=零是开环零点,D(s)是开环极点。
从稳定性的角度来看,闭环极点不必位于s平面的RH面上。特性方程如1+G(s)H(s)等于零表示闭环极点。
当1+G(s)H(s)等于零时,因此q(s)必须为零。
因此,从稳定性的角度来看,q(s)的零点不应该位于s平面的右手平面内。
为了描述强度,需要考虑整个RHP。因此,我们通过考虑趋于无穷大的半圆半径“R”,想象一个包括RHP内所有点的半圆。
用奈奎斯特图进行稳定性分析
根据奈奎斯特图,我们可以根据参数值来识别控制系统是稳定的、不稳定的还是边缘稳定的。
- 增益交叉频率和相位交叉频率。
- 增益裕度和相位裕度。
相位交叉频率。
奈奎斯特图与负实轴相交的频率称为相位交叉频率,用ωpc表示。
增益交叉频率
奈奎斯特图具有一个幅值的频率称为增益交叉频率,用ωgc表示。
以下讨论基于两个频率之间的主要关系(如相位交叉和增益交叉)的控制系统稳定性。
- 如果ωpc比ωgc高,那么控制系统是稳定的。
- 如果ωpc等于ωgc,那么控制系统是稍微稳定的。
- 如果ωpc小于ωgc,则控制系统不稳定。
增益裕度
增益裕度相当于相位交叉频率下奈奎斯特图幅度的倒数。
增益裕度(GM)=1/Mpc
其中,“Mpc”是ωpc或相位交叉频率下正常范围内的幅度
相位裕度
相位裕度相当于180度和ωgc或增益交叉频率下的相位角之和。
PM=1800+
其中,ξgc是增益交叉频率下的相位角(ωgc)。
控制系统的稳定性取决于两个裕度之间的主要关系,如下面给出的增益裕度和相位裕度。
如果增益裕度高于1且相位裕度为正,则控制系统是稳定的。
如果增益裕度等于1,相位裕度为“0”度,则控制系统稍微稳定。
如果增益裕度低于1且相位裕度为负,则控制系统不稳定。
奈奎斯特图示例问题
示例1:如果奈奎斯特图在0.6距离处切割负实轴,那么系统增益裕度是多少?
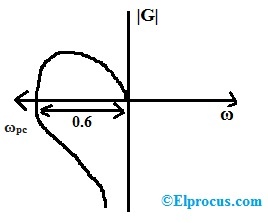
我们知道,系统的增益裕度可以定义为开环增益内使闭环系统不稳定所需的变化量
增益裕度或GM=1/|G|wpc
其中,系统的增益为|G|,wpc为相位交叉频率。
相位交叉频率可以定义为:;系统增益为“0”的频率。
Gm=1/0.6=1.66
示例2:单位增益负反馈系统的开环系统传递函数可以给出为G(s)=1/s(s+1)。S平面内的奈奎斯特曲线包括整个右侧平面和左侧原点周围的小区域,如下图所示。通过G(S)奈奎斯特图的(-1+j0)点的包围圈数量,相当于奈奎斯特轮廓,表示为“N”,然后“N”相当于?
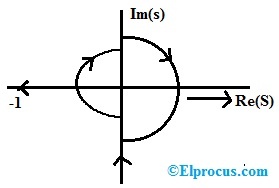
(-1+j0)有效点的包围圈数通过N=P-Z给出。
其中“N”是该临界点在逆时针方向上的包围圈数。
“P”是S平面右侧的开环极点数量。
“Z”是S平面右侧的闭环极点数量。
N=P表示稳定性Z=0。
上述公式仅在为S平面的右侧定义奈奎斯特曲线时有效,并且在源处排除极点。曲线旋转应为顺时针方向,临界点的环绕方向应为逆时针方向。
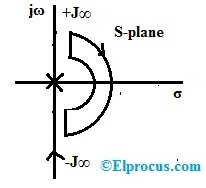
G(s)=1/s(s+1)。
开环极点存在于S=0,-1
闭环的传递函数=1/S^2+S+1
右侧闭合极点的数量为零。
但是奈奎斯特轮廓是为S平面的整个半侧定义的,并且也包含原点处的极点。
因此,在S=0时,开环极点被认为是S平面右侧内的极点。
N=P-Z=>1-0=>1
优点和缺点
这个奈奎斯特图的优点包括以下内容。
- 奈奎斯特图在确定系统稳定性方面是一个非常有用的工具。
- 它比Routh-Horwitz&root轨迹有很多优点,因为它可以简单地管理时间延迟。
- 但是,它最有帮助,因为它为我们提供了一种利用博德图来决定稳定性的方法。
- 通过使用这一点,可以决定控制系统的稳定性。
- 通过简单地测量开环传递函数的频率响应,可以找到开环传递函式。
- 与根轨迹相比,它在时间延迟方面更好,这意味着奈奎斯特图可以简单地管理系统内的时间延迟。
- 它可以定位开环传递函数的频率响应。
- 它可以在s平面的右侧找到可用极点的数量。
- 它发现了系统的相对稳定性/
这个奈奎斯特图的缺点包括以下内容。
- 奈奎斯特图利用了一些困难的数学方法。
- 它无法解决系统的全部强度问题。
- 它没有给出关于s平面右表面上可用极点的精确信息。
奈奎斯特图应用
奈奎斯特图的应用包括以下内容。
- 奈奎斯特图用于通过频域内的图形处理来建立系统稳定性。
- 奈奎斯特图或频率响应图主要用于控制工程和信号处理。
- 这些是极坐标图的扩展,用于寻找闭环控制系统的稳定性。
- 它是确定系统稳定性的一个非常有用的工具。
- 使用奈奎斯特图,我们可以监测两点(-1,0)和曲线与负实轴相交的点之间的距离。
奈奎斯特图是如何用于确定稳定性的?
稳定性可以通过使用奈奎斯特图来确定,只需查看点的包围圈数量(−1,0)。系统将稳定的各种增益可以通过观察真实的轴交叉来确定。该图提供了一些关于传递函数形状的数据。
奈奎斯特采样标准是什么?
奈奎斯特准则需要采样频率至少是信号中包含的最大频率的两倍。如果采样频率低于最高模拟信号频率的两倍,则会发生一种称为混叠的现象。
奈奎斯特图使用什么?
开环传递函数用于奈奎斯特图。
奈奎斯特法则是什么?
奈奎斯特法则简单地指出,周期性信号应该以信号最大频率分量的两倍以上进行采样。事实上,由于可用的时间有限,采样率略高于所需的采样率。
无噪声的奈奎斯特比特率公式是什么?
奈奎斯特简单地指出,在带宽为“B”的信道中,每秒可以传输多达2B个正交信号,因此,Rp≤2B,其中“Rp”是脉冲率。
奈奎斯特曲线代表什么?
奈奎斯特图表示关于传递函数形式的一些信息。例如;该图给出了传递函数的极点和零点数量通过曲线到达原点的角度之间的变化信息。
因此,这是奈奎斯特图的概述——优点、缺点及其应用。奈奎斯特图用于分析控制系统的特性,如稳定性、相位裕度和增益裕度。使用Matlab绘制奈奎斯特图帮助我们制作奈奎斯特图,该图与通过 动态模型。这里有一个问题要问你,什么是预兆情节?
