什么是特勒根定理：工作原理及其应用

在网络分析中，了解网络定理对于电路分析非常重要。因此，有不同的网络定理可用，如叠加定理、特勒根定理、诺顿定理、最大功率转移定理、戴维宁定理、补偿定理、置换定理、互易定理、米尔曼定理和米勒定理。但是理解每个网络定理是非常重要的，因为每个定理都用于特定的应用。本文讨论了网络定理的一种类型，如特勒根定理，使用示例。

特勒根定理是什么？

特勒根定理是一种网络定理，由荷兰电气工程师Bernard D.H.特勒根于1952年发明并发表。在网络分析中，与其他定理相比，这个定理是一个非常重要的定理，因为大多数网络定理都可以通过使用这个定理导出。

这个网络定理主要依赖于基尔霍夫定律。因此，这个定理可以简单地应用于遵循基尔霍夫定律的网络。这个网络定理用于具有线性、非线性、有源、无源、时变或非变元件的电路。

Tellegen的定理陈述是，“对于任何类型的网络，不同分支中不同元素使用的直接功率之和等于零（0）”。该定理基于守恒原理，因此用于生物和化学应用，以发现物理网络的主动性能，也用于设计信号处理中的滤波器，。

Telegen定理的求解步骤

使用特勒根定理求解任何电网都需要遵循以下步骤。

• 首先，我们需要定位电网中的支路电压降。
• 通过传统分析技术找到等效支路电流
• 然后，这个定理可以通过将所有支路中的电压和电流的乘积相加来证明。

交流电路的特勒根定理

特勒根定理的基本概念在交流或直流电路中是相同的。对于交流电路的应用，可以说，在任何有源或无源、线性或非线性、时变网络中，通过交流电源退出，电源的瞬时或复功率之和为零。

为了分析这个定理，考虑具有'n'个元素的网络。流经整个元件的瞬时电流为i1、i2、i3、i4…。，而该支路中的瞬时电压是v1、v2、v3、v4…。，越南盾。

因此，元件-1的瞬时电流和电压为i1&v1，通过该元件使用的瞬时功率（p1）为“v1i1”。

p1=v1*i1

对于element2，瞬时功率（p2）为

p2=v2*i2

同样，第n个元素的瞬时功率is（pn）为

pn=vn*英寸

根据特勒根定理，所有的瞬时幂和都是“0”。所以，我们需要求和所有的瞬时功率，比如p1，p2，p3，p4…。，在…上

p1+p2+p3+p4…+pn=0

v1 i1+v2 i2+v3 i3+v4i4…+vn in=0

对于第k个分支，上述方程可以用一般形式写成：；

ding="async" class="size-full wp-image-42027 aligncenter" src="https://uploads.9icnet.com/images/aritcle/20230518/Tellegens-Theorem-Equation.jpg" alt="" width="140" height="58" sizes="(max-width: 140px) 100vw, 140px">

在上述方程中，

“n”是网络中分支的总数

“vk”是“第k”支路的瞬时电压

“ik”是“k”支路的瞬时电流

“pk”是“k”分支的瞬间力量

如果我们将下图视为一个AB分支，它等效于一个k分支。

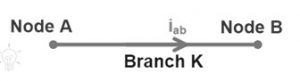
因此，瞬时电压vk=va–vb

整个a到b支路的电流瞬间流动为“ik”；

ik=iab

因此，像pk这样的瞬间力量是；

pk=vk*ik=（va–vb）iab…。。（I）

现在，我们需要考虑从b到a的相反方向的瞬时电流；

iab=–iab

瞬时电压；

vk=vb–va

瞬时功率“pk”为；

pk=vk ik=（vb–va）iba……（ii）

通过对上述i和ii方程求和，我们可以得到

2vk ik=（va–vb）iab+（vb–va）iba

vk ik=1/2[（va–vb）iab+（vb–va）iba]……。。（iii）

根据基尔霍夫电流定律，电流的代数和在电路的一个节点为零。

因此

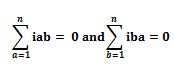
如果我们在上面的方程（iv）中代入这个值，我们得到

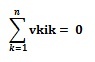
因此，经验证，输送到网络的功率总和为“0”。因此，特勒根定理得到了证明。还解释了通过网络元件吸收的功率之和等于通过源传递的功率之总和。

特勒根定理解决的问题

下面解决特勒根定理的示例问题。

示例1：验证以下直流网络的Telegen定理。

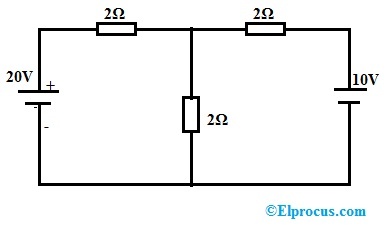
在节点上应用KCL

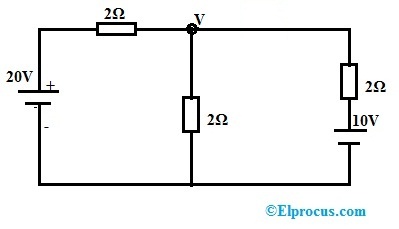
V-20/2+V/2+V-10/2=0

（V-20+V+V-10）/2=0

3V=30伏

V=30/3=10伏

当电流流过电路时

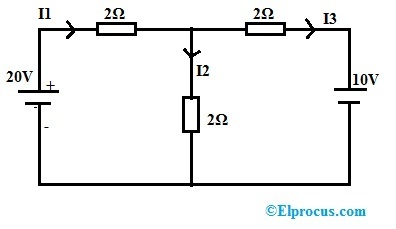
I1=20-V/2=20-10/2=10/2=5A

I2=V/2=10/2=5A

I3=V-10/2=10-10/2=0

20V电源供电，

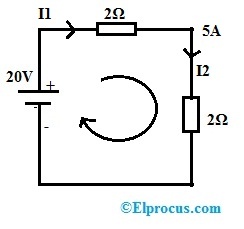
P=V x I=>20×5=100瓦

网络中无源元件吸收的功率为

P=I^2 R=>5^2×2+5^2×2

25 x 2+25 x 2=100瓦

因此，提供的功率=吸收的功率

因此，网络中所有幂的代数和等于零。

示例2：

使用特勒根定理，找到以下电路的6A电流源两端的电压。

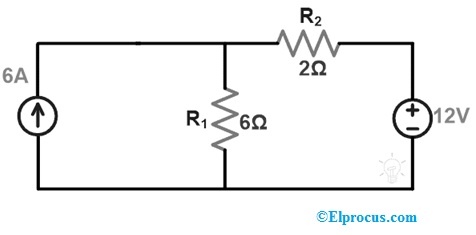
首先，我们需要通过将KVL或KCL应用于上述网络来计算流经整个电路的电流或电压。

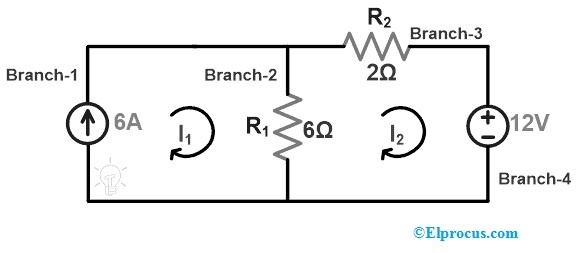
通过将KVL应用于loop-2，我们可以得到

-12=8I2–6I1

包括电流源在内的整个支路的电流为I1＝6A；

将上述方程式中的“I1”值代入；我们可以得到“I2”值。

-12=8I2–6I1

我们知道I1=6A

-12=8I2–6（6）

-12=8I2–36

8I2=36–12=>24

I2=3A

整个支路2的电流为；

I12=I1–I2=>6–3=3A

I12=3A

现在，我们需要找到每个分支的功率

P1=V I1=V x 6=6 x V

P2=R1 I12^2=6 x 9=54瓦

P3=R2 I2^2=2 x 9=18瓦

P4=伏I2=-12 x 3=-36瓦

在这里，能源有两个分支。因此，这些分支可以被认为是电力输送分支。将正（+ve）号设置为瞬时功率。

剩下的分支只有电阻器。因此，这些是功率吸收分支&将负（-）号设置为瞬时功率。

像P1和P4这样的功率都具有正号，而功率P2和P3具有负号。
现在，我们需要增加所有的瞬间力量。

P1–P2–P3+P4=0W

P1–54–18+36=108瓦

通过6A电流源传输的功率为108W。因此，6A电流源两端的电压可以通过以下方程计算。

P1=电压I

108瓦=V x 6A

V=108/6=18伏

因此，6A电流源两端的电压为18V。

KCL-KVL和特勒根定理是如何联系的？

像KVL和KCL这样的基尔霍夫定律的结果是特勒根定理。这个定理是通过KVL或KCL来验证的。

我们能在交流和直流电路上验证Thevenin定理吗？

是的，我们可以在交流和直流电路上验证Thevenin定理。与直流电路类似，这个定理可以应用于包含电阻器、电容器和电感器等线性元件的交流电路。与等效塞韦宁电阻类似，通过改变所有电压源的内部阻抗可以获得等效阻抗。

哪一个定理适用于线性电路和非线性电路？

代换定理适用于线性和非线性电路

你如何使用特勒根定理？

特勒根定理可以用来设计滤波器和复杂的操作系统。

应用

这个特勒根定理的应用包括以下内容。

• 特勒根定理用于检验困难的网络系统，如电路、代谢和生物网络、化学过程和管道运输网络。
• Tellegen定理用于设计数字信号处理（DSP）系统中的滤波器。
• 用于生物和化学过程。
• 用于反应网络结构分析和拓扑结构。
• 用于不同的石油和化工厂，以确定复杂系统的稳定性。
• 这个定理适用于具有线性/非线性、时变/非变以及有源/无源元件的电路。

因此，这一切都是关于特勒根定理、推导、示例问题及其应用的概述。特勒根定理的局限性在于，为了验证特勒根定理，使用了KVL和KCL方程。这个定理主要适用于能量守恒定律。这个定理被用在许多网络系统中。这是一个问题。叠加定理是什么？