研究背景

由二维（2D）材料制成的纳米机械谐振器为实现高性能器件提供了有趣的途径。将纳米力学与最近在2D材料中发现的磁相和电子相结合时，会产生独特的功能和现象，例如魔角诱导的相变、2D Ising反铁磁体以及2D原子层和异质结中的铁磁性。目前，只有几种方法可用于研究2D材料中的这些相。表征块材晶体中相变的一种通用方法是通过比热的反常，但是在质量小于皮克的微米级样品中很难测量。

由于这些相与机械运动密切相关，多层2D材料薄膜的温度依赖性谐振频率和品质因数在相变温度附近表现出反常。尽管机械自由度和电子自由度/电磁自由度之间的耦合似乎并不明显，但是这种耦合背后的电子/磁序和熵的变化反映在其比热中，进而导致热膨胀系数发生变化，从而影响张力和谐振频率。由于相变附近的比热将呈现不连续性，因此可以使用悬浮薄膜的温度依赖性谐振频率来探测该相变

成果介绍

有鉴于此，近日，荷兰代尔夫特理工大学Makars Šiškins、Herre S. J. van der Zant和Peter G. Steeneken（共同通讯作者）等证明了二维反铁磁性FePS3、MnPS3和NiPS3薄膜中的相变可以通过与温度相关的谐振频率和品质因数进行机械探测。观察到的机械运动与反铁磁序之间的关系是由比热介导的，并且揭示了FePS3的Néel温度对静电感应应变的强烈依赖性。同时，正如在2H-TaS2中探测电子电荷密度波相所证明的那样，该方法不限于磁序。因此，该方法提供了在各种材料中表征相变的潜力，包括反铁磁和绝缘等传统表征方法不适用的材料。文章以“Magnetic and electronic phase transitions probed by nanomechanical resonators”为题发表在著名期刊Nature Communications上。

图文导读

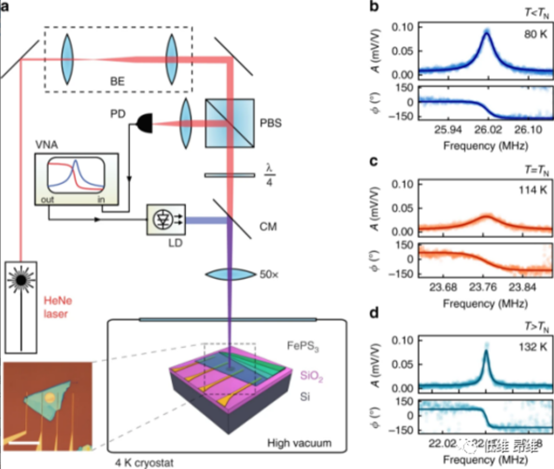
反铁磁性FePS3薄膜中机械谐振的表征。（a）激光干涉测量装置。（b-d）在三个不同温度下，基本谐振的振幅（A）和相位（ϕ）。

图1. 反铁磁性FePS3薄膜中机械谐振的表征。（a）激光干涉测量装置。（b-d）在三个不同温度下，基本谐振的振幅（A）和相位（ϕ）。

FePS3是一种Ising型反铁磁体，块材的Néel温度在TN~118-123 K的范围内，并且在TN附近的比热表现出明显的特征。使用机械剥离和干法转移，将FePS3薄片转移到Si晶圆上蚀刻的圆形腔上。厚度在8到45 nm之间的悬浮式FePS3器件被放置在低温恒温器中，并冷却至4 K。然后，使用激光干涉技术（图1a）对谐振频率进行表征。在4至200 K的温度范围内测量基本薄膜模式的共振频率f0（T）。图1b-d分别给出了反铁磁相（80 K），相变附近（114 K）和顺磁相（132 K）的典型谐振。

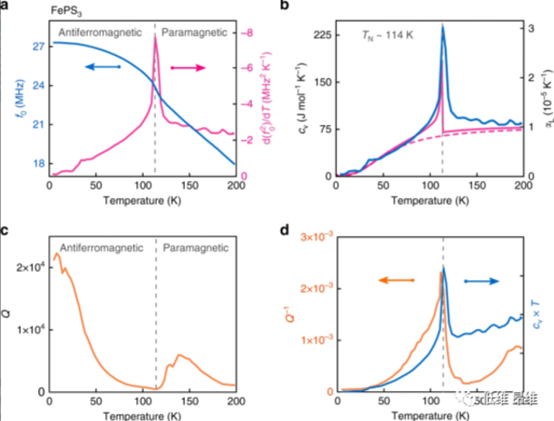
FePS3谐振器的机械和热性能，薄膜厚度为45.2±0.6 nm。

图2. FePS3谐振器的机械和热性能，薄膜厚度为45.2±0.6 nm。（a）蓝色实线-谐振频率与温度的关系，品红色实线-f02的温度导数。（b）蓝色实线-实验得出的比热和相应的热膨胀系数，品红色实线-磁比热的理论计算。（c）薄膜基本谐振的机械品质因数Q（T）。（d）橙色实线-测量的机械阻尼Q-1（T）随温度的变化，蓝色实线-归一化的cv（T）T项。

图2a给出了同一FePS3薄膜的f0（T）（蓝色实线），在相变附近观察到振幅、谐振频率和品质因数的显著变化。首先分析f0与比热之间的关系。图2a中，谐振频率随温度升高而降低，表明由于薄膜的热膨胀而引起应变降低。f0（T）负斜率的最陡峭部分在114 K附近出现一个大峰值（品红色实线），将此温度定义为TN并用垂直虚线表示。在图2b中显示了FePS3的比热曲线（蓝色实线），将该结果与比热的理论模型（品红色实线）进行比较，实验数据和理论数据之间存在紧密对应关系，表明相变附近的杨氏模量变化可忽略不计，并且FePS3的cv（恒定体积下的比热）反常导致了观察到的谐振频率变化。

随后，分析了图2c和d中的品质因数数据。恰好在TN之上，随着温度从114 K升高到140 K，显著的品质因数（图2c）表现出显著增加。在相变附近观察到的品质因数最小值表明，材料中的耗散与热力学有关，并且可能与热弹性阻尼有关。由于从谐振频率分析中获得了cv（T）的估算值（图2b），因此将实验耗散Q-1（T）与cv（T）T曲线进行比较。测得的耗散和热弹性项均在TN~114 K附近存在一个峰值。这两个量之间的紧密定性对应关系表明，与热弹性阻尼相关的项确实可以解释相变附近Q（T）的温度依赖性。

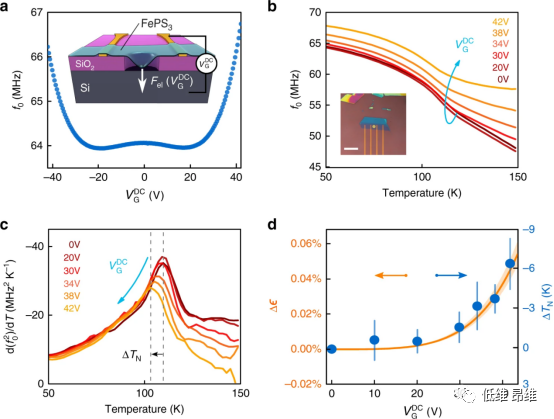
谐振频率和转变温度通过栅极电压调控

图3. 谐振频率和转变温度通过栅极电压调控。（a）在50 K下，谐振频率与栅极电压的关系。插图：静电调谐原理的示意图。（b）对于六个不同的电压，谐振频率与温度的关系。（c）f02的导数与栅极电压和温度的关系。（d）蓝色实心点-TN随VGDC的变化，橙色实线-静电感应应变Δϵ与VGDC的函数模型。

由于磁矩之间距离相关的相互作用系数ζ（ϵ），相变温度与应变相关。为了验证这种效果，使用了8±0.5 nm的FePS3样品，悬浮在直径为4 μm的空腔上。在材料和底部Si衬底之间施加栅极电压VGDC以引入静电力，将薄膜拉下并使其拉紧。如图3a所示，薄膜的谐振频率随栅极电压遵循W形曲线。这是由于两个抵消作用：在较小的栅极电压下，会发生薄膜的电容性软化，而在较高的电压下，薄膜的张力会由于施加的静电力而增加，从而导致谐振频率增加。图3b显示了六个不同栅极电压下的f0（T），随着VGDC增大，f0（T）最陡斜率点的移动在图3b中清晰可见，并且图3c中的峰在静电力引起的应变作用下向下移动6 K。这是由于拉伸应变引起了层间距离增加，导致磁矩耦合减小，降低了TN（图3d）。

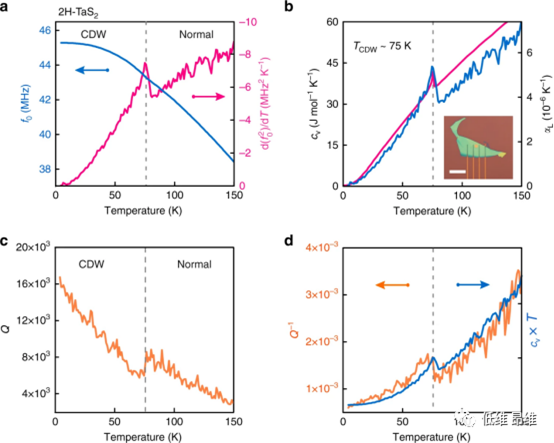
2H-TaS2谐振器的机械性能，薄膜厚度为31.2±0.6 nm，d=4 μm

图4. 2H-TaS2谐振器的机械性能，薄膜厚度为31.2±0.6 nm，d=4 μm。（a）蓝色实线-谐振频率与温度的关系，品红色实线-f02的温度导数。（b）蓝色实线-cv和热膨胀系数随温度的变化，品红色实线-块材2H-TaS2的比热。（c）品质因数Q（T）随温度的变化。（d）橙色实线-测量的机械阻尼Q-1（T）随温度的变化，蓝色实线-归一化的cv（T）T项。

由于材料中的比热和有序参量之间的耦合具有一般的热力学性质，只要该材料的弹性特性和Grüneisen参数与温度的关系很小，那么本方法可适用于多种材料。为了证明该方法能够探测到电子相变，研究了2H-TaS2在TCDW~77 K时的电荷密度波（CDW）转变。图4a给出了f0（T）和f02的温度导数，其中峰值为75±3 K。图4b显示了比热在75 K处的向下台阶（蓝色实线），表明从CDW到无序高温状态的相变，与在块材晶体中测得的cv的定量关系接近。Q因子还显示出一个局部最小值，在转变温度附近有一个下降（图4c）。如前所述，预计Q-1（T）与cv（T）T将遵循相同的趋势，在图4d中也表现出良好的定性对应关系。

总结与展望

本文证明了在二维材料的超薄薄膜中机械运动与电子/磁序之间存在强耦合。在本研究中，推导了材料比热与温度相关谐振频率之间关系的解析方程，并与实验结果非常吻合。同时，由于材料以悬浮状态使用，排除了衬底对材料电子和磁性的影响。该方法不仅可以用于表征反铁磁和绝缘材料超薄薄膜，还可以利用相关材料的独特性能来开发器件概念，有望实现多功能应用。