补偿定理:工作、例子及其应用
在网络理论中,研究或了解其中一个分支的阻抗变化的影响是非常重要的。因此,它会影响电路或网络的相应电流和电压。所以补偿定理是。。。
在网络理论中,研究或了解其中一个分支的阻抗变化的影响是非常重要的。因此,它会影响电路或网络的相应电流和电压。因此,补偿定理被用来了解网络内部的变化。这个网络定理简单地适用于欧姆定律的概念,该概念指出,只要在整个电阻器上提供电流,那么电阻器上就会有一定量的电压下降。因此,这个电压降将抵抗电压源。因此,我们以与电压源相反的极性连接一个额外的电压源&其大小相当于电压降。本文讨论了补偿定理–使用应用程序。
什么是补偿定理?
网络分析中的补偿定理可以定义为:;在网络中,任何电阻都可以用包括零内阻的电压源来代替,该电压等效于由于流过电阻的电流而导致的电阻两端的电压降。
让我们假设整个“R”电阻器的电流“I”和电压下降,因为电阻器上的电流为(V=I.R)。根据补偿定理,这个电阻器通过产生电压的电压源来代替,电压将指向网络电压方向或电流方向。
补偿定理解决的问题
下面给出了补偿定理的示例问题。
示例1:
对于以下电路
1). 当电阻为4Ω时,求出整个AB支路的电流。
2). 当电阻3Ω变为9Ω时,用补偿定理求出整个AB支路的电流。
3). 验证补偿定理。
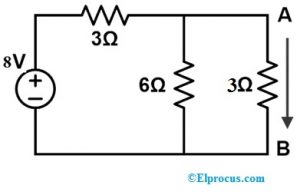
解决方案:
如上面的电路所示,3Ω和6Ω这样的两个电阻器并联,而且这种并联组合只是与3Ω电阻器串联,那么电阻就会相等;
Re1=6||3+3=>(6×3/6+3)+3
= (18/9) + 3 => 2+3 = 5 Ω.
基于欧姆定律;
8=I(5)
I=8÷5
I=1.6 A
现在,我们必须找到整个AB分支的电流。因此,基于电流分配器的规则;
I’=1.6(6)/6+3=>9.6/9=1.06A
2). 现在我们必须将3Ω电阻器改为9Ω电阻器。根据补偿定理,我们应该在与9Ω电阻器串联的范围内包括一个新的电压源&电压源值为;
VC=I'ΔZ
哪里
ΔZ=9–3=6Ω&I’=1.06 A。
VC=(1.06)x 6Ω=6.36V
VC=6.36伏
修改后的电路图如下所示。
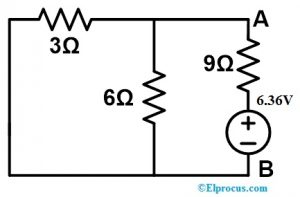
现在我们必须找到等效电阻。因此,像3Ω和6Ω这样的电阻器只是简单地并联连接。之后,这种并联组合通过一个9Ω的电阻器简单地串联连接。
需求=3||6+9
需求=(3×6||3+6)+9
需求=(18||9)+9
需求=(2)+9
要求=11欧姆
基于欧姆定律;
V=ΔI x R
6.36=ΔI(11)
ΔI=6.36÷11
ΔI=0.578 A
因此,基于补偿定理;电流内的变化为0.578A。
3). 现在,我们必须通过用9Ω电阻器计算以下电路中的电流来证明补偿定理。因此,修改后的电路如下所示。在这里,像9Ω和6Ω这样的电阻器并联连接,这种组合通过3Ω电阻器简单地串联连接。
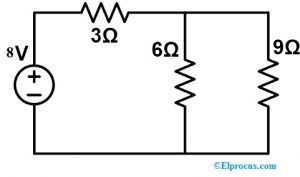
REq=9 | | 6+3
REq=(6×9|6+9)+3
REq=(54|15)+3
REq=45+54/15=>99/15=>6.66欧姆
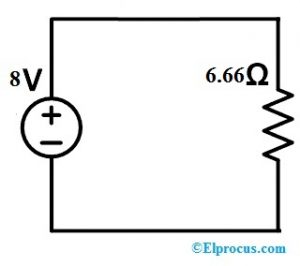
来自上面的电路
8=I(6.66)
I=8÷6.66
I=1.20A
基于电流分配器规则;
I’=1.20(6)/6+9
I’=1.20(6)/6+9=>7.2/15=>0.48A
ΔI=I'–I“
ΔI=1.06-0.48=0.578A
因此,证明了补偿定理,即电流内的变化是根据该定理计算的,该定理类似于从实际电路测量的电流内变化。
示例2:
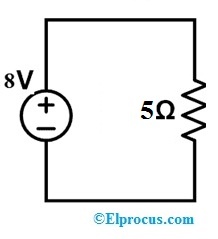
以下电路A和B的两个端子中的电阻值修改为5欧姆,那么补偿电压是多少?
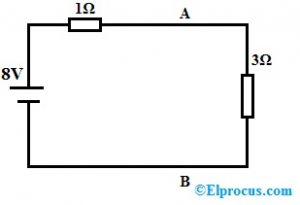
对于上述电路,首先,我们需要应用KVL
-8+1i+3i=0
4i=8=>I=8/4
I=2A
ΔR=5Ω-3Ω
ΔR=2Ω
补偿电压为
Vc=I[ΔR]
Vc=2×2
Vc=4伏
交流电路中的补偿定理
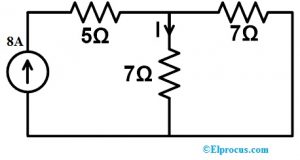
如果用补偿定理将3欧姆电阻器替换为7欧姆电阻器,则找出以下交流电路中的电流变化,并证明该定理。
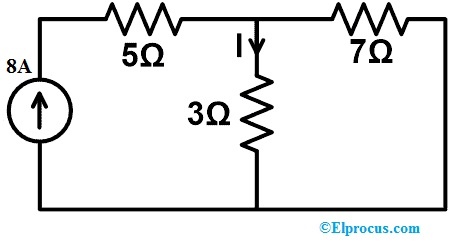
上述电路仅包括电阻器以及单独的电流源。因此,我们可以将这个定理应用于上述电路。所以这个电路是通过电流源供电的。因此,现在我们必须在KVL或KCL的帮助下找到整个3Ω电阻器分支的电流。尽管如此,通过使用电流分配器规则可以很容易地找到这种电流流动。
因此,基于电流分配器规则;
I=(8(7)/7+3)A=>56/10A=>5.6A。
在具有3欧姆电阻器的实际电路中,整个支路的电流为7A。所以我们必须把这个3欧姆的电阻换成7欧姆。由于这种变化,整个支路的电流也将发生变化。现在我们可以用补偿定理找到电流的变化。
为此,我们必须设计一个补偿网络,通过简单地断开电流源和短路电压源来去除网络中所有可用的独立电源。在这个电路中,我们只有一个电流源,这是一个理想的电流源。因此,我们不需要包括内部阻力。对于这个电路,我们需要做的下一个修改是包括一个额外的电压源。所以这个电压值是;
VC=IΔZ=>7×(7–3)
VC=7×4=>28伏
现在,具有电压源的补偿电路如下所示。
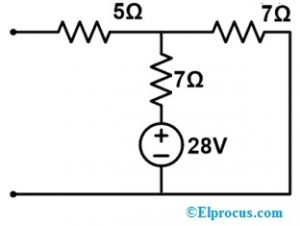
该电路仅包括一个回路,其中整个7Ω支路的电流供应将为我们提供电流变化,即(∆i)。
ΔI=VC÷(7+7)=>28÷14=>2 A
为了证明这个定理,我们必须通过连接一个7Ω的电阻器来找到电路内的电流,如下面的电路所示。
I“=(8(7))÷(7+7)
I“=56÷14
I“=4 A
现在应用电流分配器规则;
为了找到电流的变化,我们需要从通过原始网络的电流中减去这个电流。
ΔI=I–I“
ΔI=7–4=>3 A
因此,补偿定理得到了证明。
为什么我们需要一个补偿定理?
- 补偿定理非常有用,因为它提供了有关网络内变化的信息。这个网络定理还允许我们在网络的任何分支中找到精确的电流值,一旦网络在一个步骤中被直接替换为任何特定的变化。
- 通过使用这个定理,我们可以得到网络元素内微小变化的近似效果。
优势
这个补偿定理的优点包括以下内容。
- 补偿定理提供了关于网络内的变化的信息。
- 这个定理基于欧姆定律的基本概念。
- 一旦在电路中调整了电阻值,它就有助于发现电压或电流的变化。
应用
这个补偿定理的应用包括以下内容。
- 该定理经常用于获得电网元件内的近似小变化效应。
- 这对于分析桥梁网络的灵敏度尤其有用。
- 该定理用于分析分支元素的值发生变化的网络,也用于研究对这些值的容差效应。
- 一旦网络在一个步骤中被直接替换为任何特定的更改,您就可以在任何联网分支中确定正确的当前值。
- 该定理是网络分析中最重要的定理,用于计算电网的灵敏度和求解电网和电桥。
因此,这是网络分析中补偿定理的概述——示例问题及其应用。因此,在这个网络定理中,任何电路中的电阻都可以通过电压源来改变,当改变的电阻两端的电压下降时,电压源具有类似的电压。这里有一个问题,什么是叠加定理?
