代换定理:求解步骤、例题及其应用
网络分析中使用的基本网络定理有不同类型,如Thévenin定理、叠加定理、Norton定理、代换定理、最大功率转移定理、互易定理和Millman定理。每一个定理,它们。。。
网络分析中使用的基本网络定理有不同类型,如Thévenin定理、叠加定理、Norton定理、代换定理、最大功率转移定理、互易定理和Millman定理。每个定理都有自己的应用领域。因此,理解每个网络定理是非常重要的,因为这些定理可以在不同的电路中重复使用。这些定理帮助我们求解给定条件下的复杂网络电路。本文讨论了网络定理的一种类型代换定理–示例。
什么是置换定理?
置换定理的陈述是;只要知道整个支路的电流或网络中任何支路的电压,就可以通过不同元件的组合来改变支路,从而在整个支路中产生类似的电压和电流。换句话说,它可以定义为;对于支路的等效性,热电压和电流应该是相同的。
代换定理的概念主要取决于一个元素与另一个元素的代换。这个定理对证明其他一些定理也很有帮助。尽管这个定理不适用于求解包括上述两个既不串联也不并联的源的定理。
替换定理的解释
求解代换定理所涉及的步骤主要包括以下几个方面。
第1步:首先,我们需要找到所有网络元件的电压和电流。通常,电压和电流可以借助欧姆定律、Kirchoff定律(如KVL或KCL)进行计算。
第2步:选择您希望通过不同的元件(如电压源/电阻和电流源)移除的所需分支。
第3步:在电压和电流不应改变的情况下,找到被替换元件的正确值。
步骤4:通过简单地计算所有元件的电流和电压来检查新电路,并通过原始网络进行评估。
替换定理电路图
通过使用下面的电路图,让我们很容易理解代换定理。我们知道替换定理是用另一个等价元素替换单个元素。如果网络中的任何元件被电流源或电压源取代,其整个元件或元件两端的电流和电压将像以前的网络一样保持不变。
像R1、R2和R3这样的各种电阻简单地连接在电压源两端。流经电路的电流“I”分为I1和I2,其中“I1”流经“R1”电阻,“I2”流经R2电阻,如电路所示。这里,电阻R1、R2和R3两端的电压降相应地为V1、V2和V3。
现在,如果“R3”电阻被“V3”电压源取代,如以下电路图所示:

在下面的电路图中,“R3”电阻被整个元件“I1”的电流所取代。

从以上两种情况来看,如果用电流或电压源替换元件,那么电路的初始条件不会改变,也就是说,即使用其他源替换,电阻两端的电压供应和整个电阻的电流供应也不会改变。
问题示例
下面将讨论替换定理的示例问题。
示例1:
用代换定理求解以下电路,以计算所有电阻器内的电压和电流。

第1步:
首先,将KVL应用于上述电路中的回路1
14=6I1–4I2…。(1)
向上述电路中的回路2施加KVL
0=12I2–4I1
12 I2=4I1=>I1=3I2………。(2)
将该方程式2代入上述方程式1中。
14=6(3I2)–4I2
14=18I2–4I2=>14I2=>1A
I2=1A
根据上述方程-(2)
I1=3I2
我们知道I2=1A
I1=3A
第2步:
在这一步中,我们需要删除loop1分支以形成一个单独的循环。

第3步:
我们可以用电流源/电压源代替4Ω电阻器。现在,我们将使用电流源。
整个回路中回路2的电流为1A。因此,我们用1A电流源代替支路。因此,剩余电路如下所示。

第4步:
在这个步骤中,需要检查所有元件的电压和电流。上述电路包括单个回路,即电流源。因此,整个回路中流动的电流值与电流源值相似。
这里,电流源的值是1A。因此,整个3Ω和5Ω电阻器分支的电流为1A,这与原始网络类似。
使用欧姆定律,找到3Ω电阻器两端的电压值
V=红外线
V=I x R
V=1 x 3=>3V。
同样,通过使用欧姆定律,我们需要找到5Ω电阻器上的电压值。
V=红外线
V=I x 5
V=1 x 5=>5伏。
因此,电流和电压与原始网络相似。这就是这个定理的工作原理。
现在,如果我们在步骤3中选择电压源来代替电流源。因此,在这种情况下,电压源的值与4Ω电阻器分支的值相似。
原始网络内4Ω电阻器支路的电流为
I1–I2=>3–1=>2A
根据欧姆定律;
4Ω电阻器处的电压为V=2 x 4=8V
因此,我们需要在网络中连接8V的电压源&剩余电路如下图所示。
V=2 x 4=8伏
因此,我们需要将8V电压源与网络连接,剩余电路如下图所示。

向上述回路施加KVL,以验证电压和电流。
8=3I+5I=>8I
I=1A。
通过使用欧姆定律,电阻器3Ω两端的电压可以计算为:;
V=1×3=>3V
同样,电阻器5Ω两端的电压为;
V=1×5=>5伏
因此,替换后的电压和电流与原始网络相同。
示例2:
让我们用下面的电路来应用代换定理。
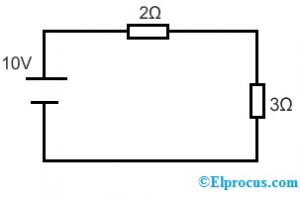
根据分压尺,2Ω和3Ω电阻器两端的电压为;
3Ω电阻器处的电压为
V=10×3/3+2=6伏
2Ω电阻器处的电压为
V=10×2/3+2=4伏
整个电路的电流计算为I=10/3+2=2A。
在上述电路中,如果我们用6V电压源代替3Ω电阻器,那么电路将变成如下所示。

根据欧姆定律,2Ω电阻器两端的电压和整个电路的电流为
V=10-6=>4伏
I=10-6/2=2A
如果我们用2A电流源代替3Ω电阻器,那么电路将变成如下所示。

2Ω电阻器两端的电压为V=10–3*2=>4 V,“2A”电流源两端的电压是V=10-4=>6 V。因此,2Ω电阻器之间的电压和整个电路的电流没有变化。
优势
这个代换定理的优点包括以下内容。
- 这个定理的概念主要取决于一个元素与另一个元素的替换。
- 这个定理提供了电路行为的直觉,也有助于验证其他各种网络定理。
- 使用这个定理的优点是,这个定理为对应于交点的变量(如X和Y)提供了正确的值。
局限性
这个代换定理的局限性包括以下内容。
- 该定理不能用于求解包含至少两个或两个以上不在串联/并联范围内的源的网络。
- 在这个定理中,当替换元件时,电路行为不应该改变。
应用
这个代换定理的应用包括以下内容。
- 替代定理被用来证明许多其他定理。
- 这个定理对求解数学方程组很有帮助。
- 这个定理将电路的一个元素替换为另一个元素。
- 这个定理被用来分析具有相关源的电路。
哪一个电路的代换定理不适用?
如果电路具有以上两个并联或串联的源,则此替换定理不适用。
为什么补偿定理被称为置换?
补偿和替换这两个定理在过程和归约方面是相同的。所以这个定理适用于天线,也被称为替代定理。
你如何使用代换定理?
这个定理可以通过将网络中的任何分支替换为不同的分支来使用,而不会干扰整个网络中的电压和电流。所以这个定理既适用于线性电路,也适用于非线性电路。
什么是置换性质?
替换属性规定,如果变量“a”等效于另一个变量“b”,则可以在任何表达式或方程式中替换“a”来代替“b”&可以在任何公式或方程式中取代“b”代替“a”。
因此,这一切都是关于替代定理的概述——电路和例子。这里有一个问题,补偿定理是什么?
